About me

Welcome! I am an assistant professor in the Department of Industrial Engineering and Management Sciences (IEMS) and the Department of Mechanical Engineering (ME) at Northwestern University. I obtained my Ph.D. from the Department of Industrial and Operations Engineering at the University of Michigan. The research in our lab is driven by the need for novel statistical and optimization methodologies addressing scientific and engineering challenges across diverse domains, including distributed data ecosystems, Digital Twins, and smart manufacturing. We are also interested in investigating the theoretical underpinnings of these methods. In particular, our current research in personalized, collaborative, and decentralized data analytics explores computational techniques to integrate knowledge from multiple sources.

Featured papers

A few topics of my research are introduced below.

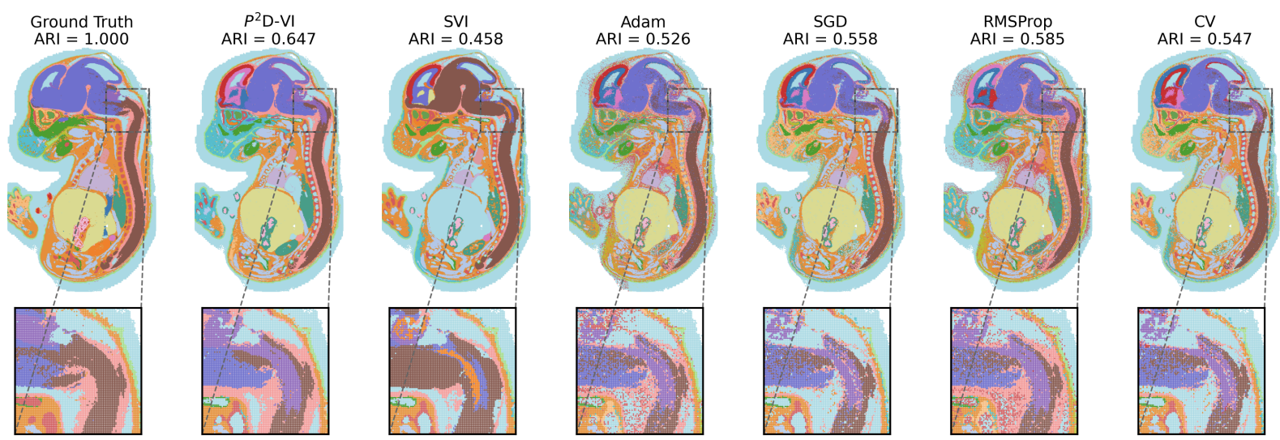
Scalable Mean-Field Variational Inference via Preconditioned Primal-Dual Optimization Jinhua Lyu, Tianmin Yu, Ying Ma, Naichen Shi, 2026. Link.

The scale and complexity of modern Bayesian statistics are growing. While Mean Field Variational Inference (MFVI) offers an efficient approach to probabilistic inference, it struggles to handle hierachical models where the number of latent variables grows with the number of data points. We developed a mini-batch version of MFVI and introduced a primal-dual algorithm, PD-VI, along with its block-preconditioned extension, P²D-VI. These methods utilize an augmented Lagrangian formulation to jointly update global and local parameters while adapting to heterogeneous loss geometries.

Mouse

On a spatial transcriptomics domain detection task, P²D-VI is capable of segmenting transcriptomic profiles across over 150,000 locations in under 6 seconds.

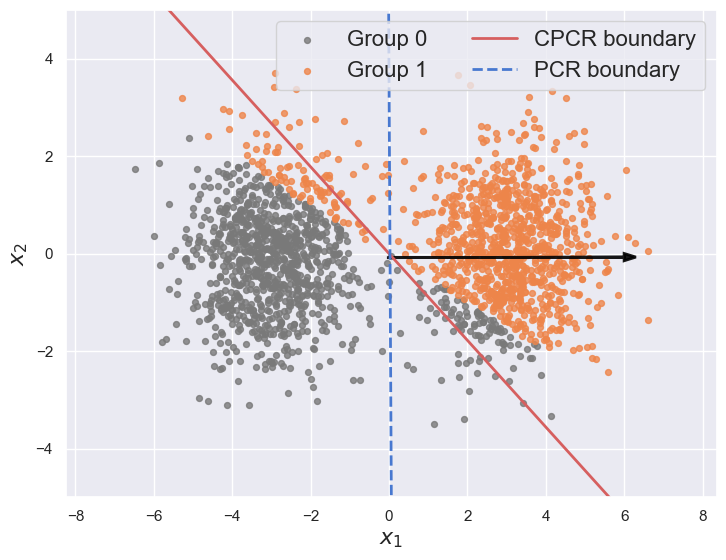
Calibrated Principal Component Regression Yixuan Florence Wu, Yilun Zhu, Lei Cao, Naichen Shi, 2025. Link.

When we reduce the dimension of the input data using PCA, we reduce data complexity by retaining only most relevant information. However, using only top PCA embeddings for downstream analytics, such as regression, always brings risks as meaningful information in the remaining PCs could be discarded.

CPCR

We introduce a Calibrated Principal Component Regression model that leverages cross-fitting to restore some information lost in PCA. A risk analysis grounded the random matrix theory reveals the optimal tradeoff between bias and variance.

Here is a more comprehensive list of publications. You can also check my Google scholar profile.

Naichen Shi

Featured papers

Recent news