About me

Welcome! I am an assistant professor in the Department of Industrial Engineering and Management Sciences (IEMS) and the Department of Mechanical Engineering (ME) at Northwestern University. I obtained my Ph.D. from the Department of Industrial and Operations Engineering at the University of Michigan. The research in our lab is driven by the need for novel statistical and optimization methodologies addressing scientific and engineering challenges across diverse domains, including distributed data ecosystems, Digital Twins, and smart manufacturing. We are also interested in investigating the theoretical underpinnings of these methods. In particular, our current research in personalized, collaborative, and decentralized data analytics explores computational techniques to integrate knowledge from multiple sources.

Featured papers

A few topics of my research are introduced below.

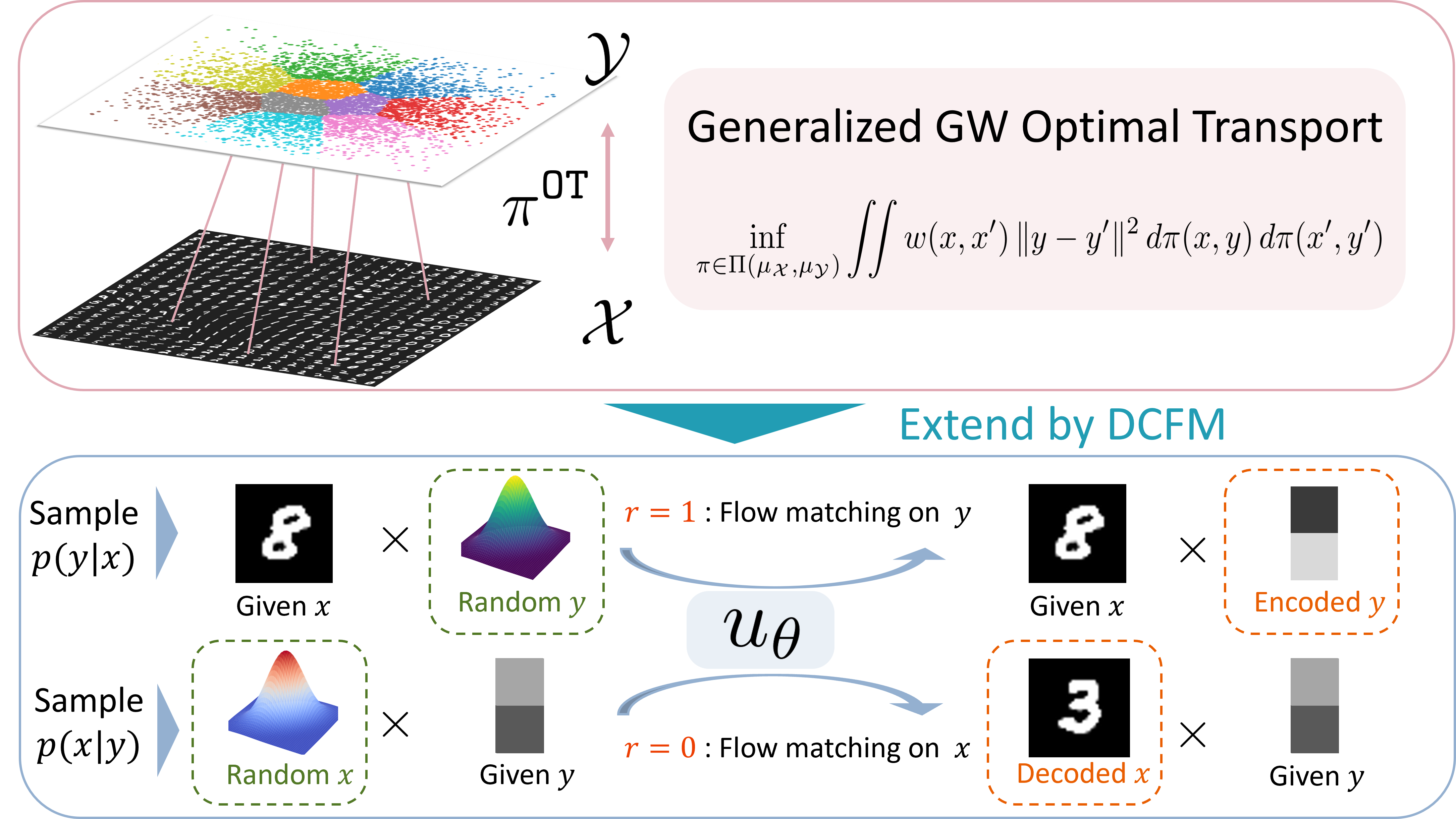
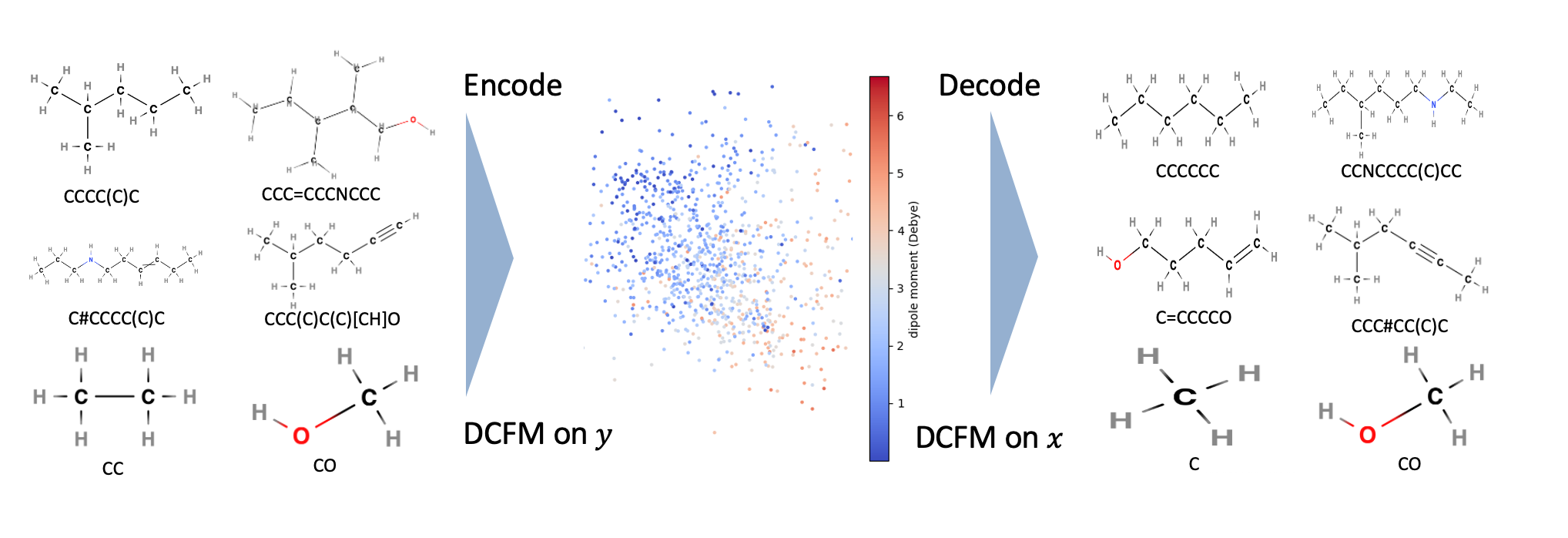
Coupled Flow Matching Wenxi Cai, Yuheng Wang, Naichen Shi, 2025. [Link pending].

Many nonlinear dimension-reduction methods, such as EigenMaps, t-SNE, UMAP, and VAEs, map high-dimensional data into informative low-dimensional embeddings. But what if we want to explicitly control the distribution of these embeddings?

CPFM

We develop a Coupled Flow Matching framework that unifies optimal transport and generative modeling. It consists of two components: an efficient solver for a generalized form of Gromov-Wasserstein optimal transport, and a dual conditional flow-matching network that learns bidirectional mappings between data and embeddings. Together, they enable mapping complex, high-dimensional data into controllable low-dimensional representations, and generating realistic data samples from them.

QM9

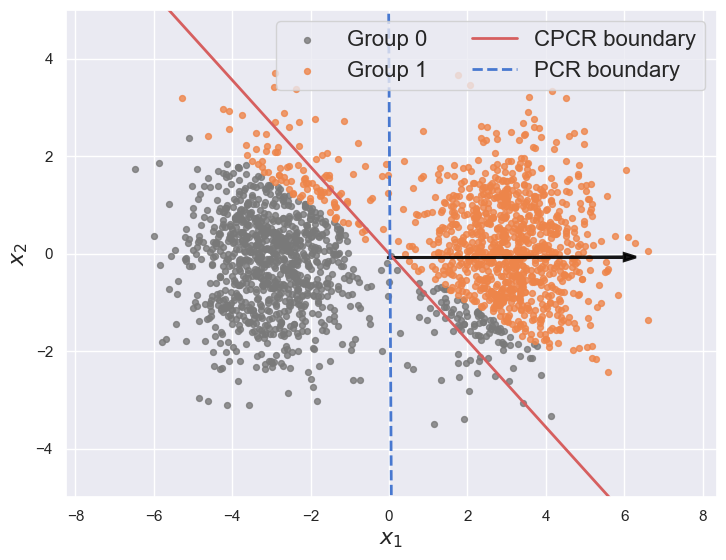
Calibrated Principal Component Regression Yixuan Florence Wu, Yilun Zhu, Lei Cao, Naichen Shi, 2025. Link.

When we reduce the dimension of the input data using PCA, we reduce data complexity by retaining only most relevant information. However, using only top PCA embeddings for downstream analytics, such as regression, always brings risks as meaningful information in the remaining PCs could be discarded.

CPCR

We introduce a Calibrated Principal Component Regression model that leverages cross-fitting to restore some information lost in PCA. A risk analysis grounded the random matrix theory reveals the optimal tradeoff between bias and variance.

Here is a more comprehensive list of publications. You can also check my Google scholar profile.

Naichen Shi

Featured papers

Recent news